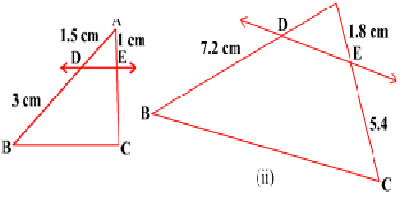
1.   In Fig. 6.17, (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).




2.   E  and  F  are  points  on  the  sides  PQ  and  PR respectively of a ∆PQR.
 For each of the following cases, 
state whether EF || QR :
(i)   PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm

(ii)   PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm

(iii)   PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm

3.   In Fig., if  LM || CB and LN || CD,





A 
 B
C 
 D
M 
L 
N 




 prove that

    ${AM}/{AB}={AN}/{AD}$
	
4.   In Fig., DE || AC and DF || AE.





A 
 C
B 
 D
E 
F 


 Prove that ${BF}/{FE}={BE}/{EC}$

5.   In Fig.  DE || OQ and DF || OR. 






P 
Q
R 
 O
E 
F 
D 




Show that  EF || QR.
	 
6.   In Fig. 6.21, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR.
	 



P 
Q
R 
O 
A 
B 
C 




	 
	 Show that BC || QR.
	 
7.   Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle 
	parallel to another side bisects the third side.
	 
8.   Using Theorem 6.2, prove that the line joining the mid-points of any two sides of a triangle is 
      parallel to the third side.
	  
9.   ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. 
     Show that ${AO}/{BO}={CO}/{DO}$
	 
10. The diagonals of a quadrilateral ABCD intersect each other at the point O such that
    ${AO}/{BO}={CO}/{DO}$.Show that ABCD is a trapezium.