Two triangles are similar, if
(i) their corresponding angles are equal and
(ii) their corresponding sides are in the same ratio (or proportion).


That is, in ∆ABC and ∆ DEF, if
(i) ∠A = ∠ D, ∠B = ∠ E, ∠ C = ∠F and
(ii) ${AB}/{DE}={BC}/{EF}={CA}/{FD}$ ,
then the triangle's are similiar.

Here, A corresponds to D, B corresponds to E and C corresponds to F. Symbolically, we write the similarity of these two triangles as ‘∆ ABC ~ ∆ DEF’ and read it as ‘triangle ABC is similar to triangle DEF’. The symbol ‘~’ stands for ‘is similar to’.

Activity 4 : Draw two line segments BC and EF of two different lengths, say 3 cm and 5 cm respectively. Then, at the points B and C respectively, construct angles PBC and QCB of some measures, say, 60° and 40°. Also, at the points E and F, construct angles REF and SFE of 60° and 40° respectively (see Fig. 6.23).



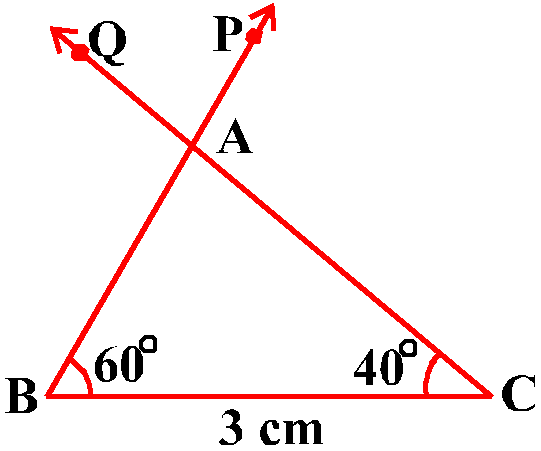
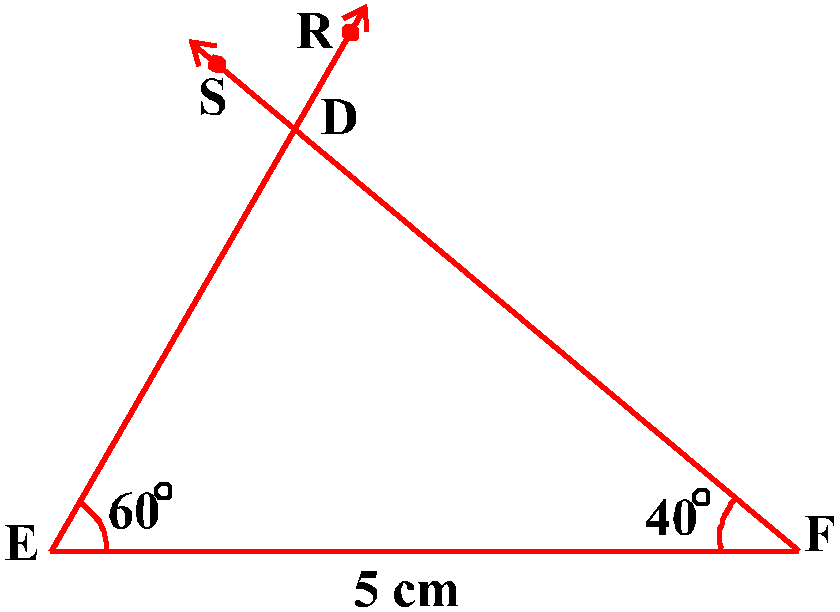
Let rays BP and CQ intersect each other at A and rays ER and FS intersect each other at D. In the two triangles ABC and DEF, you can see that ∠ B = ∠ E, ∠ C = ∠ F and ∠A = ∠ D. That is, corresponding angles of these two triangles are equal. What can you say about their corresponding sides ? Note that ${BC}/{EF}=3/5=0.6$
What about ${AB}/{DE}$ and ${CA}/{FD}$? On measuring AB, DE, CA and FD, you will find that,
${AB}/{DE}$ and ${CA}/{FD}$ are alos equal to 0.6.
Thus, ${AB}/{DE}$ = ${BC}/{EF}$= ${CA}/{FD}$
You can repeat this activity by constructing several pairs of triangles having their corresponding angles equal. Every time, you will find that their corresponding sides are in the same ratio (or proportion). This activity leads us to the following criterion for similarity of two triangles.

This criterion is referred to as the AAA (Angle–Angle–Angle) criterion of similarity of two triangles. This theorem can be proved by taking two triangles ABC and DEF such that
∠A = ∠ D, ∠ B = ∠ E and ∠ C = ∠ F (see Fig.)


Proof

Cut DP = AB and DQ = AC and join PQ.
So, ∆ ABC ≅ ∆ DPQ
This gives ∠ B = ∠ P = ∠ E and PQ || EF
Therefore, ${DP}/{PE}={DQ}/{QF}$
i.e ${AB}/{DE}={AC}/{DF}$
Similarly, ${AB}/{DE}={ BC}/{EF}$ and so ${AB}/{DE}={ BC}/{EF}={AC}/{DF}$

Remark : If two angles of a triangle are respectively equal to two angles of another triangle, then by the angle sum property of a triangle their third angles will also be equal.