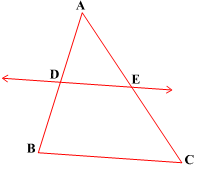
Theorem 6.2 : If a line divides any two sides of a triangle in the same ratio,
then the line is parallel to the third side.
Proof
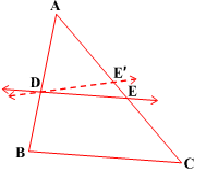
This theorem can be proved by taking a line DE such that ${AD}/{DB}={AE}/{EC}$ and assuming that DE is not parallel to BC (see Fig.) If DE is not parallel to BC, draw a line DE′ parallel to BC. So, ${AD}/{DB}={AE'}/{E'C}$ Therefore ${AE}/{EC}={AE'}/{E'C}$ Adding 1 to both sides of above, you can see that E and E′ must coincide.
Example 1: If a line intersects sides AB and AC of a ∆ABC at D and E respectively and is parallel to BC, prove that ${AD}/{AB}={AE}/{AC}$Solution :
Given: DE || BC So, ${AD}/{DB}={AE}/{EC}$ or, ${DB}/{AD}={EC}/{AE}$ Add 1 on both side, ${DB}/{AD}+1={EC}/{AE}+1$ or ${AB}/{AD}={AC}/{AE}$ So, ${AD}/{AB}={AE}/{AC}$ ;Hence Proof
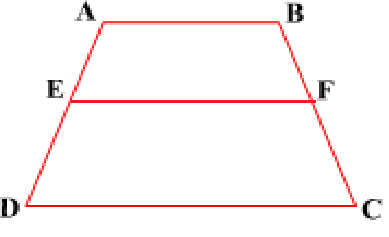
Example 2 : ABCD is a trapezium with AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF is parallel to AB,Show that ${AE}/{ED}={BF}/{FC}$
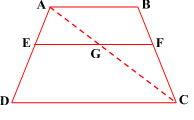
Solution : Join AC to intersect EF at G (see Fig.).
Given:AB || DC and EF || AB So, EF || DC (Lines parallel to the same line are parallel to each other) Now, in ∆ADC, EG || DC (As EF || DC) So, ${AE}/{ED }={AG}/{GC} ............(1)$ Similarly, from ∆CAB, ${CG}/{AG}={CF}/{BF}$ i.e ${AG}/{GC}={BF}/{FC} ............(2)$ Therefore, from (1) and (2), ${AE}/{ED }={BF}/{FC}$
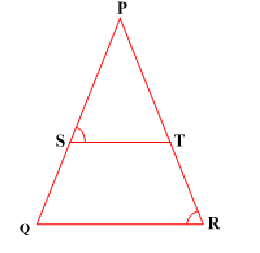
Example 3: In Fig. ${PS}/{SQ}={PT}/{TR}$ and ∠PST =∠ PRQ. Prove that PQR is an isosceles triangle.
Solution : Given: ${PS}/{SQ}={PT}/{TR}$ So,ST || QR Therefore, ∠ PST = ∠ PQR (Corresponding angles)...........(1) Also, it is given that ∠ PST = ∠ PRQ .................................(2) So, ∠ PRQ = ∠ PQR [From (1) and (2)] Therefore, PQ = PR (Sides opposite the equal angles) i.e., PQR is an isosceles triangle.