Two triangles are similiar, if
(i)  their  corresponding  angles  are  equal  and
(ii)  their  corresponding  sides  are  in  the  same  ratio  (or  proportion).





If  corresponding  angles  of  two triangles  are  equal,then  they  are  known  as equiangular triangles. 
The  ratio  of  any  two  corresponding  sides  in two  equiangular  triangles  is  always  the  same.

Basic  Proportionality Theorem
Activity

Activity  :  Draw any angle XAY and on its one arm AX, mark points (say five points) P, Q, D, R and B 
such that AP = PQ = QD = DR = RB.  



Now, through B, draw any line intersecting arm AY at C (see Fig.).
Also, through the point D, draw a line parallel to BC to intersect AC at E. 
Observe that ${AD}/{DB}=3/2$. Also observe that ${AE}/{EC}$ is also equal to $3/2$.
This is called Basic  Proportionality Theorem.

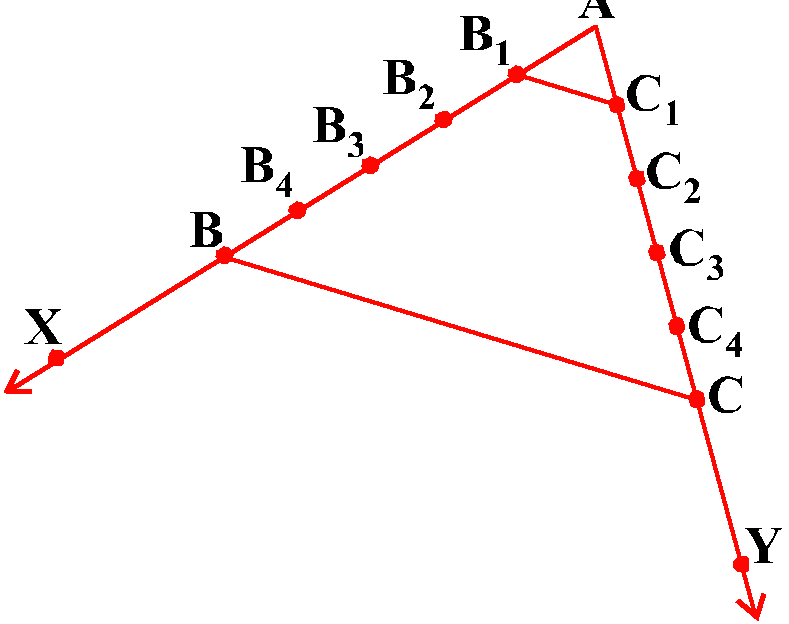
Proof : We are given a triangle ABC in which a line parallel to side BC intersects other two sides AB and AC 
at D and E respectively (see Fig).


Prove that ${AD}/{DB}$=${AE}/{EC}$

Proof Click 
Join BE and CD and draw DM ⊥AC and EN ⊥ AB.
Now, area of ∆ADE (= $1/2$× base × height)=$1/2$×AD × EN.
 area of ∆ADE is denoted as ar(ADE).
Similarly,ar(BDE)=$1/2$×DB × EN
          ar(ADE)= $1/2$×AE × DM.
	and   ar(DEC)= $1/2$×EC × DM.
	
Therefore ${ar(ADE)}/{ar(BDE)}$=${1/2×AD × EN}/{1/2×DB × EN}$=${AD}/{DB} ...(1)$

and ${ar(ADE)}/{ar(DEC)}$=${1/2×AE × DM}/{1/2×EC × DM}$=${AE}/{EC} ......(2)$

Note that ∆ BDE and DEC are on the same base DE and between the same parallels
BC and DE.
So,                          ar(BDE) =  ar(DEC) .............(3) 

Therefore, from (1), (2) and (3), we have :
            ${AD}/{DB}$=${AE}/{EC}$
			
Is  the  converse  of  this  theorem  also  true.
To examine this, let us perform the following activity:


Activity:Draw  an  angle  XAY  on  your notebook and on ray AX, mark points $B_1, B_2, B_3, B_4$ 
 and B such that $AB_1=B_1B_2=B_2B_3=B_3B_4=B_4B$.
 Similarly,  on  ray  AY,  mark  points
$C_1, C_2, C_3, C_4$   and C such that $AC_1  = C_1C_2  = C_2C_3   =  C_3C_4   =  C_4C$. 
 Then  join  $B_1C_1$   and  BC (see Fig. )



Note that ${AB_1}/{B_1B}$=${AC_1}/{C_1C}$ (Each equal to $1/4$)
You  lines $B_1C_1$  and BC are parallel to each other, i.e., $B_1C_1$ ||  BC ...(1)                                    
(1) Similarly, by joining $B_2C_2$, $B_3C_3$ and $B_4C_4$, you can see that:
      ${AB_2}/{B_2B}$=${AC_2}/{C_2C}$$(=2/3)$ and $B_2C_2$ ||  BC ......(2)
      ${AB_3}/{B_3B}$=${AC_3}/{C_3C}$$(=3/2)$ and $B_3C_3$ ||  BC ......(3)
      ${AB_4}/{B_4B}$=${AC_4}/{C_4C}$$(=4/1)$ and $B_4C_4$ ||  BC ......(4)
	  
 From (1), (2), (3) and (4), it can be observed that if a line divides two sides of a triangle in the same ratio,
 then the line is parallel to the third side.
 
 You can repeat this activity by drawing any angle XAY of different measure and taking any  number of equal parts
 on arms AX and AY . Each time, you will arrive at the same result. Thus, we obtain the following theorem, 
 which is the converse of Theorem 6.1: