That is quadrilateral ABCD is similar to the quadrilateral PQRS if,
(i)∠A = ∠P, ∠ B = ∠Q, ∠ C = ∠ R, ∠ D = ∠ S and
(ii) ${AB}/{PQ}$=${BC}/{QR}$=${CD}/{RS}$=${DA}/{SP}$

Example
Find whether the following quadrilateral ABCD and PQRS are similiar.


Solution
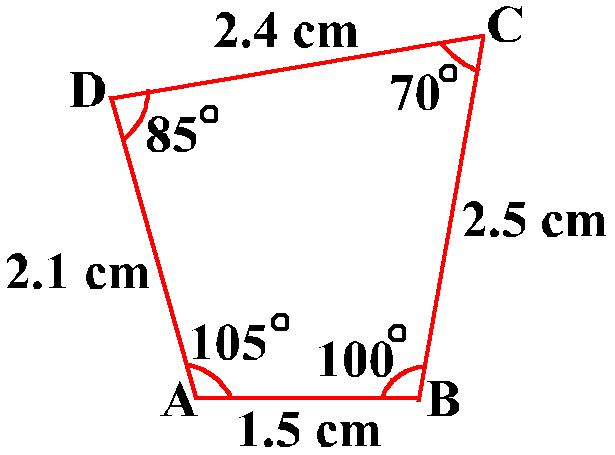
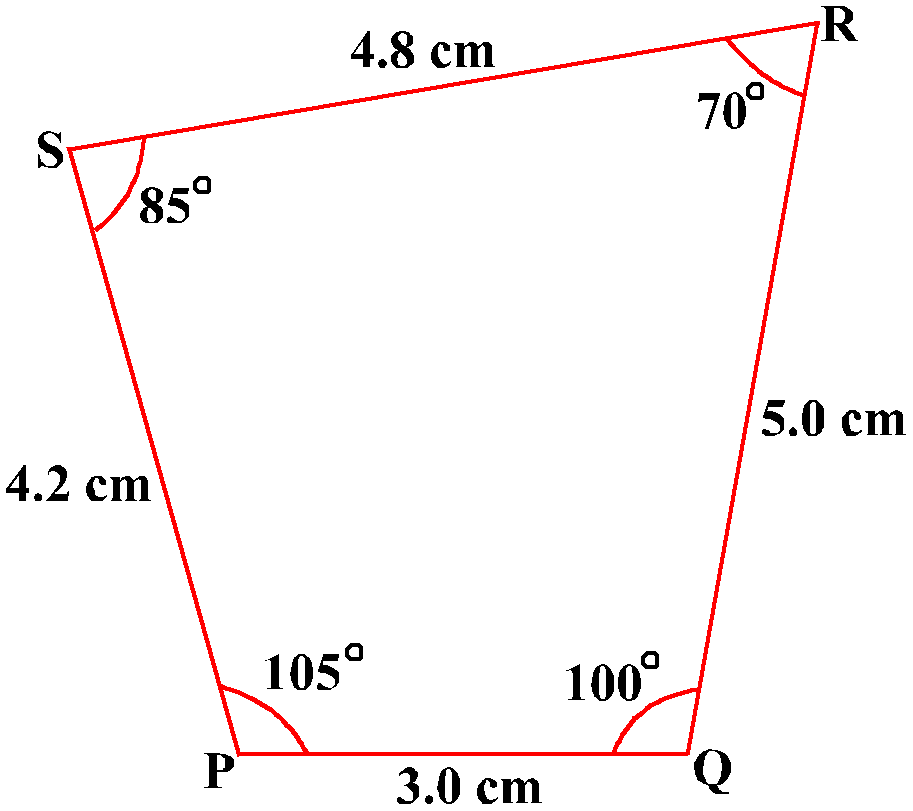
We can say that ABCD and PQRS is similiar if,
(i) ∠A = ∠P, ∠ B = ∠Q, ∠ C = ∠ R, ∠ D = ∠ S and
(ii) ${AB}/{PQ}$=${BC}/{QR}$=${CD}/{RS}$=${DA}/{SP}$

Verifing condition (i)
∠A = 105⁰
∠P = 105⁰
Therefore ∠A = ∠P;

∠ B = 100⁰
∠Q = 100⁰
Therefore ∠ B = ∠Q

∠ C = 70⁰
∠ R = 70⁰
Therefore ∠ C = ∠ R

∠ D = 85⁰
∠ S = 85⁰
Therefore ∠ D = ∠ S

The above quadrilaterals are satisting condition (i).

Verifing condition (ii)
${AB}/{PQ}$= $1.5/3$=$2$

${BC}/{QR}$=$2.5/5$=$2$

${CD}/{RS}$=$2.4/4.8$=$2$

${DA}/{SP}$=$2.1/4.2$=$2$

Since ${AB}/{PQ}$=${BC}/{QR}$=${CD}/{RS}$=${DA}/{SP}$ , so the quadrilaterals are satisting condition(ii)

Ans:Since both the conditions are satisfied, quadrilateral ABCD and PQRS are similiar.