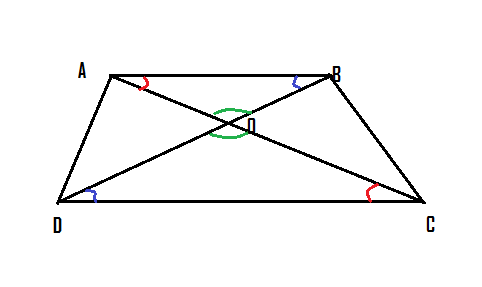
1.   Let ∆ABC ~ ∆ DEF and their areas be, respectively, 64 $cm^2$  and 121 $cm^2$. If EF =15.4 cm,
     find BC.

Solution
If two triangles  ∆ABC  and  ∆DEF are similar, then 
${ar(ABC)}/{ar(DEF)}=({AB}/{DE})^2= ({BC}/{EF})^2 = ({CA}/{DF})^2$
$64/121 = ({BC}/{15.4})^2$
$√(64/121) = ({BC}/{15.4})$
${BC}/15.4 = 8/11$
$BC = 11.2$ $cm$


2.   Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O.
     If AB = 2 CD, find the ratio of the areas of triangles AOB and COD. 

Solution


In trapezium ABCD, AB || DC, and AC and BD are diagonals.
Therefore 
          ∠BAO =  ∠DCO
		  ∠ABO =  ∠CDO
		  ∠AOB =  ∠COD
Therefore by AAA criteria, ∆AOB is similiar to ∆COD.
${ar(ABC)}/{ar(COD)}=({AB}/{DC})^2$ = $(2/1)^2$ =$4/1$
		 
3.   In Fig.,ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, 
	 
	Show that ${ar (ABC)}/{ar (DBC)}={AO}/{DO}$

Solution


In fig. ABC and DBC are two triangles on the same base BC.
Let AP and DM are two perpendiculars drawn to base BC.
${arc(ABC)}/{arc(DBC)}$ = ${1/2× BC× AP}/{1/2 ×BC× DM}$
${arc(ABC)}/{arc(DBC)}$ = ${ AP}/{DM}$  ..........(1)

In ∆APO and ∆DMO,
		∠APO =∠DMO 
		∠AOP = ∠DOM
		
Therefore by AA similiarity , ∆APO ~ ∆DMO
$.^{.}.$ ${AP}/{DM}={AO}/{DO}$
Substituting in eqn (1), we get
${arc(ABC)}/{arc(DBC)}$ = ${ AO}/{DO}$
Hence Proved
	 
4.   If the areas of two similar triangles are equal, prove that they are congruent.

Solution
Let the triangle be ∆ABC and ∆DEF.
Since the triangles are similiar,
therefore 
        ${ar(ABC)}/{ar(DEF)}=({AB}/{DE})^2= ({BC}/{EF})^2 = ({CA}/{DF})^2$
Since the area's of two triangles are equal, so,
$1=({AB}/{DE})^2= ({BC}/{EF})^2 = ({CA}/{DF})^2$
$({AB}/{DE})= 1$ => $AB=DE$
$ ({BC}/{EF}) = 1$ => $BC = EF $
$({CA}/{DF})= 1$  => $CA = DF $

Also since the triangle be ∆ABC and ∆DEF are similiar,
	∠A = ∠D
	∠B = ∠E
	∠C = ∠F

So, if  two triangles are congruent then they will have exactly the same three sides 
and exactly the same three angles. 

Therefore ∆ABC and ∆DEF are congruent. 
Hence Proved.
		
5.   D, E and F are respectively the mid-points of sides AB, BC and CA of ∆ABC. 
     Find the ratio of the areas of ∆DEF and ∆ABC.

Solution


In ∆ABC , D, E, F are the midpoint of the side AB, BC and CA.
Therefore in triangles, ∆ABC and ∆DBE, since DE || AC,
           ∠BAC = ∠BDE
		   ∠ACB = ∠DEB
		   ∠ABC = ∠DBE
Therefore by AAA criteria, ∆ABC and ∆DBE are similiar.
Hence ${ar(BDE)}/{ar(ABC)} = ({BD}/{AB})^2$
Since BD = $1/2$AB
${ar(BDE)}/{ar(ABC)} = 1/4$
	 
6.   Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of 
     their corresponding medians.

Solution


Let ∆ABC ~ ∆PQR. AD and PS be the medians of the triangle.
Therefore ${AB}/{PQ}={BC}/{QR}={CA}/{RP}$ .....(1)
and ∠A =∠P , ∠B=∠Q , ∠C=∠R     .............(2)

AD and PS are medians of the triangles.
Therefore ,  $BD=DC=1/2{BC}$
and  $QS=SR=1/2QR$
therefore eqn (1) becomes,
${AB}/{PQ}={BC}/{QR}={CA}/{RP}$ => ${AB}/{PQ}={BD}/{QS}={CA}/{RP}$

In ∆ABD and ∆PQS, 
	∠B=∠Q ,
	${AB}/{PQ}={BD}/{QS}$ 
	
so, by SAS similiarity , ∆ABD ~ ∆PQS 
Therefore,
     ${AB}/{PQ}={BD}/{QS}={DA}/{SP}$
	 
and ${ar(∆ABC)}/{ar(∆PQR)}$ = ${AB^2}/{PQ^2}={BC^2}/{QR^2}={CA^2}/{RP^2}$

Since ${AB}/{PQ} = {DA}/{SP}$

Therefore, ${ar(∆ABC)}/{ar(∆PQR)}$  = ${AD}^2/{PS}^2$ 
Hence Proved 

	 
7.   Prove that the area of an equilateral triangle described on one side of a square is equal to half the
	area of the equilateral triangle described on one of its diagonals.

Solution


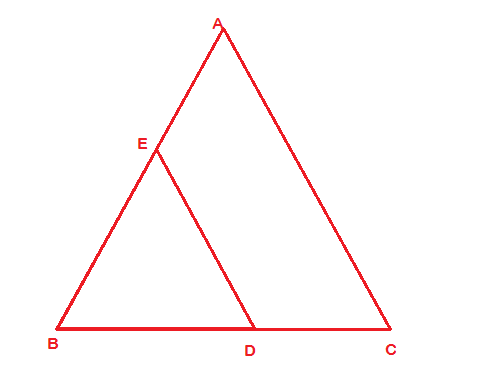
Let ABCD be the square with sides $a$ unit. 
Therefore, diagonal = √2$a$ unit

Let the equilateral triangle formed by one side of the square be ∆ABE.
and the equilateral triangle formed by one of the diagonal be ∆BDF.

The length of each sides of the ∆ABE will be $a$ unit 
and  length of each sides of the ∆BDF will be √2$a$ unit 

Since both the triangles are equilateral triangles, therefore ∆ABE~∆BDF
Therefore ${ar(ABE)}/{ar(BDF)}$ = $({a}/{√2a})^2$  => $1/2$
	
Tick the correct answer and justify :
8.   ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of
	 triangles ABC and BDE is
	(A)  2 : 1                    (B)  1 : 2                    (C)  4 : 1                    (D)  1 : 4

Solution


Both the triangles are equilateral and each angles are $60^0$.
Therefore by AAA similarity, ∆BCA~∆BDE.
Let the sides of ∆ABC be $x$ ,
Therefore the sides of ∆BDE = $x/2$ 
		${ar(ABC)}/{ar(BDE )}$ = $(x/{x/2})^2$ => $4/1$


	
9.   Sides of two similar triangles are in the ratio 4 : 9.Areas of these triangles are in the ratio
	(A)  2 : 3                    (B)  4 : 9                    (C)  81 : 16                    (D)  16 : 81

Solution
FOr similar triangles,
         ratio of areas of triangles = square of the ratio of corresponding sides,
		 i.e = $(4/9)^2$
		 i.e = $16/81$
Ans: D => $16/81$