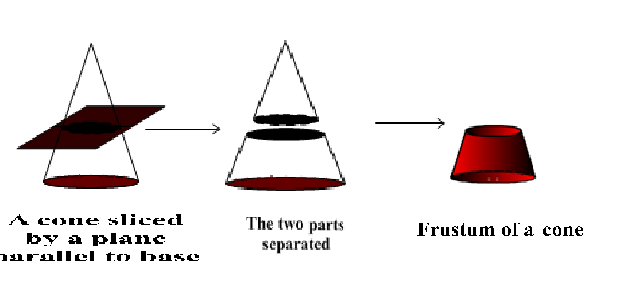
Frustum of a Cone: Given a cone, when we slice (or cut) through it with a plane parallel to its base (see Fig. 13.20) and remove the cone that is formed on one side of that plane, the part that is now left over on the other side of the plane is called a frustum* of the cone.


Example: The radii of the ends of a frustum of a cone 45 cm high are 28 cm and 7 cm (see Fig. 13.21). Find its volume, the curved surface area and the total suface area (Take π = $22/7$).

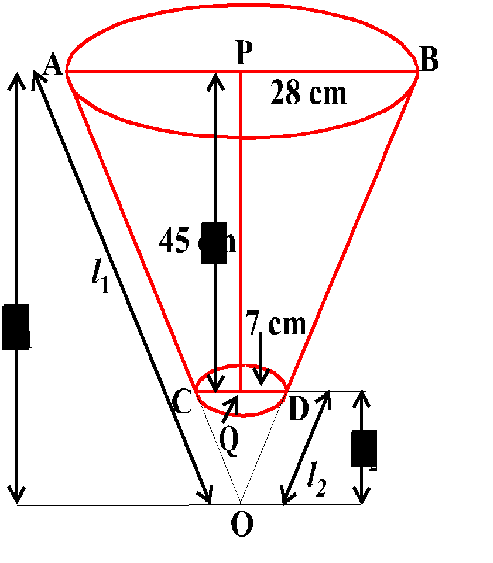
Solution : The frustum can be viewed as a difference  of  two  right  circular  cones  OAB  and OCD (see Fig. 13.21). 

Let the height (in $cm$) of the cone OAB be $h_1$  and its slant height $l_1$, i.e., OP = $h_1$  and OA = OB = $l_1$. 

Let $h_2$  be the height of cone OCD and $l_2$  its slant height.

We have : $r_1$  = 28 cm, $r_2$  = 7 cm and the height of frustum (h) = 45 cm. 
Also, $h_1= 45 + h_2$ .................(1)
We first need to determine the respective heights h1  and h2  of the cone OAB and  OCD.
Since the triangles OPB and OQD are similar , we have
				${h_1/h_2}=28/7=4/1$  ....................(2)
		
From (1) and (2)
			 $h_1=60$ and $h_2=15$
			 
Now, the volume of the frustum =  volume of the cone OAB – volume of the cone OCD
			=$({1/3}×22/7× 28^2 × 60)$ - $({1/3}×22/7× 7^2 × 15)$ 
			= 48510 $cm^3$
			
The respective slant height $l_2$  and $l_1$  of the cones OCD and OAB are given by
			$l_2 = √{(7)^2   + (15)^2}$ = 16.55 $cm$
			$l_1 = √{(28)^2   + (60)^2}$ = 66.20 $cm$
			
Thus, the curved surface area of the frustum = $πr_1l_1$  – $πr_2l_2$
											=$(22/7 × 28 ×66.20) $ - $(22/7 × 7 × 16.55)$
											= 5461.5 $cm^2$

Now, the total surface area of the frustum = the curved surface area + $πr_1^2$   + $πr_2^2$ 
											= 5461.5 $cm^2$+ $22/7 × (28)^2 $ $cm^2$ + $22/7 × (7)^2$ $cm^2$
											= 5461.5 $cm^2$ + 2464 $cm^2$ + 154  $cm^2$
											= 8079.5 $cm^2$
											
Let  $h$  be  the  height,  $l$  the  slant  height  and  $r_1$   and  $r_2$   the  radii  of  the  ends ($r_1$   >  $r_2$)  of
 the  frustum  of  a  cone.  Then  we  can  directly  find  the  volume,  the curved surace area and the total 
 surface area of frustum by using the formulae given below :
						
			(i)  Volume of the frustum of the cone    =   $1/3{πh(r_1^2   + r_2^2 + r_1r_2 )}$
							
			(ii)  the  curved  surface  area  of  the  frustum  of  the  cone  =  $ π(r_1  +  r_2)$ $l$
													where $l= √{h^2  + (r_1  − r_2 )^2  }$
													
			(iii)  Total surface area of the frustum of the cone =$ πl (r_1 + r_2) $+ $πr_1^2$   + $πr_2^2$ ,
												where $l= √{h^2  + (r_1  − r_2 )^2  }$

Homework: Hanumappa and his wife Gangamma are busy making jaggery out of sugarcane juice. They have processed the sugarcane juice to make the molasses, which is poured into moulds in the shape of a frustum of a cone having the diameters of its two circular faces as 30 cm and 35 cm and the vertical height of the mould is 14 cm . If each cm3 of molasses has mass about 1.2 g, find the mass of the molasses that can be poured into each mould .


(Answer: 13.97 kg)

Homework: An open metal bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same me- tallic sheet (see Fig. 13.23). The diameters of the two circular ends of the bucket are 45 cm and 25 cm, the total vertical height of the bucket is 40 cm and that of the cylindrical base is 6 cm. Find the area of the metallic sheet used to make the bucket, where we do not take into account the handle of the bucket. Also, find the volume of water the bucket can hold.

(The area of metallic sheet used =4860.9 cm²; volume of water =33.62 litres )