Example: Shanta runs an industry in a shed which is in the shape of a cuboid surmounted by a half cylinder (see Fig. 13.12). If the base of the shed is of dimension 7 m × 15 m, and the height of the cuboidal portion is 8 m, find the volume of air that the shed can hold. Further, suppose the machinery in the shed occupies a total space of 300 m3, and there are 20 workers, each of whom occupy about 0.08 m3 space on an average. Then, how much air is in theshed? (Take π = $22/7$)


Solution : The volume of air inside the shed (when there are no people or machinery) is given by the volume of air inside the cuboid and inside the half cylinder, taken together.
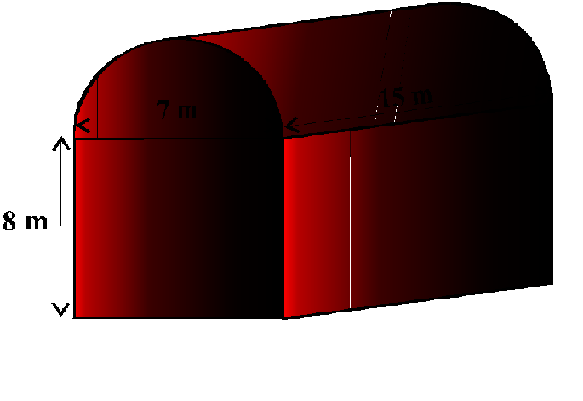
Now, the length, breadth and height of the cuboid are 15 m, 7 m and 8 m, respectively. Also, the diameter of the half cylinder is 7 m and its height is 15 m.
So, the required volume = volume of the cuboid +$1/2$ volume of the cylinder

=$({15 × 7 × 8 }+{1/2} × {22/7} × {7/2} × {7/2} × 15)$ $m^3$

=1128.75 $m^3$

Next, the total space occupied by the machinery = 300 $m^3$

And the total space occupied by the workers = 20 × 0.08 m3 = 1.6 $m^3$

Therefore, the volume of the air, when there are machinery and workers = 1128.75 – (300.00 + 1.60) = 827.15 $m^3$


Example: A juice seller was serving his customers using glasses as shown in Fig. 13.13. The inner diameter of the cylindrical glass was 5 cm, but the bottom of the glass had a hemispherical raised portion which reduced the capacity of the glass. If the height of a glass was 10 cm, find the apparent capacity of the glass and its actual capacity. (Use π = 3.14.)


Solution : Since the inner diameter of the glass = 5 cm and height = 10 cm, the apparent capacity of the glass = $πr^2h$

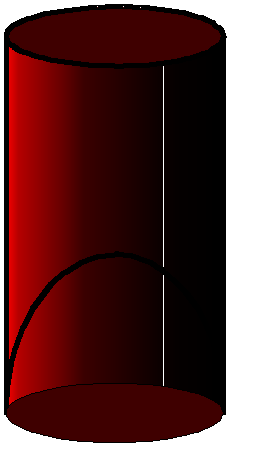
= 3.14 × 2.5 × 2.5 × 10 $cm^3$ = 196.25 $cm^3$
But the actual capacity of the glass is less by the volume of the hemisphere at the base of the glass.
i.e., it is less by $2/3{πr^3 }$ =$2/3{× 3.14 × 2.5 × 2.5 × 2.5 }$ $cm^3$= 32.71 $cm^3$

So, the actual capacity of the glass = apparent capacity of glass – volume of the hemisphere

                           =  (196.25 – 32.71) $cm^3$ = 163.54 $cm^3$ 

Example: A solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of the cone is 2 cm and the diameter of the base is 4 cm. Determine the volume of the toy. If a right circular cylinder circumscribes the toy, find the difference of the volumes of the cylinder and the toy. (Take π = 3.14)


Solution : Let BPC be the hemisphere and ABC be the cone standing on the base of the hemisphere (see Fig. 13.14).
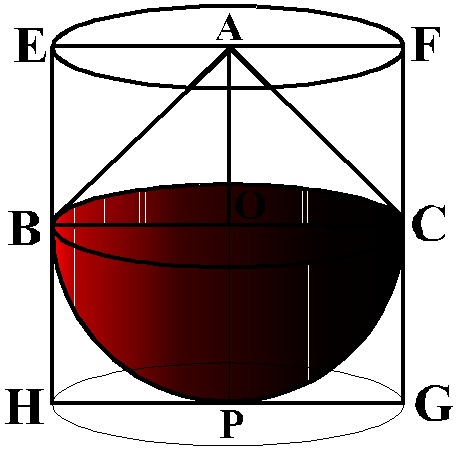
The radius BO of the hemisphere (as well as of the cone) = $1/2 × 4 $ $cm$ =$2$ $cm$

So, volume of the toy = volume of hemisphere + volumn of cone

                       =${2/3}πr^3$ + ${1/3}πr^2h$
		=$(2/3 × 3.14 × (2)^3 + 1/3 × 3.14 × (2)^2  × 2)$ $cm^3$ = 25.12 $cm^3$
				

Now, let the right circular cylinder EFGH circumscribe the given solid. The radius of the base of the right circular cylinder = HP = BO = 2 cm, and its height is

		 EH =  AO + OP = (2 + 2) cm = 4 cm
So, the volume required = volume of the right circular cylinder – volume of the toy
						=  (3.14 × 22  × 4 – 25.12) $cm^3$
						=  25.12 $cm^3$												
 

Hence, the required difference of the two volumes = 25.12 $cm^3$.