Useful Formula:


Shape
Curved Surface Area
Total Surface Area
Volumn
Cuboid 
$2(lb+bh+lh)$
$lbh$
Cube 
$6a^2$
$a^3$

Right Circular Cylinder
$2πrh$
$2πr(h+r)$
$πr^2h$
Right Circular Cone 
$πrl$
$πr(r+l)$
$1/3πr^2h$ where $l= √(h^2+r^2)$
Sphere
$4πr^2$
$4/3πr^3$
Solid Hemisphere
$2πr^2$
$3πr^2$
$2/3πr^3$
Hollow Hemisphere
$2πr^2$
$2πr^2$
$2/3πr^3$

Example: Rasheed got a playing top (lattu) as his birthday present, which surprisingly had no colour on it. He wanted to colour it with his crayons. The top is shaped like a cone surmounted by a hemisphere (see Fig 13.6). The entire top is 5 cm in height and the diameter of the top is 3.5 cm. Find the area he has to colour. (Take π = $22/7$ )


click
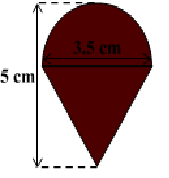
Solution : This top is exactly like the object we have discussed in Fig. 13.5. So, we can conveniently use the result we have arrived at there. That is :

Total Surface Area of the toy = Curved Surface Area of hemisphere + Curved Surface Area of cone

Now, the curved surface area of the hemisphere = $1/2(4πr^2)$ =${2πr^2}$

					=${2×(22/7)×(3.5/2)×(3.5/2)}$  $cm^2$
Also, the height of the cone = height of the top – height (radius) of the hemispherical part
						=$(5-3.5/2)$ $cm$ =3.25 $cm$
		So, the slant height of the cone (l ) = $√{r^2+h^2}$  =  $√{(3.5/2)^2+(3.25)^2}$ =3.7 $cm$
	
		Therefore, CSA of cone = πrl = $(22/7 × 3.5/2  × 3.7 )$   $cm^2$ 

		This gives the surface area of the top as: 
				=${2×(22/7)×(3.5/2)×(3.5/2)}$  $cm^2$ + $(22/7 × 3.5/2  × 3.7 )$ $cm^2$ 
				= 39.6 $cm^2$  

Example: The decorative block shown in Fig. 13.7 is made of two solids — a cube and a hemisphere. The base of the block is a cube with edge 5 cm, and the hemisphere fixed on the top has a diameter of 4.2 cm. Find the total surface area of the block. (Take π = $22/7$ )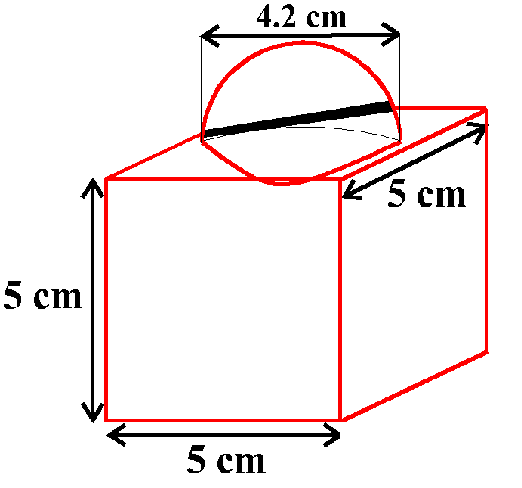

Solution : The total surface area of the cube = 6 × (edge)2  = 6 × 5 × 5 $cm^2$ = 150 $cm^2$.
 Note that the part of the cube where the hemisphere is attached is not included in the surface  area.
 So, the surface area of the block =  TSA of cube – base area of hemisphere + CSA of hemisphere
                                   =$150 – πr^2  + 2 πr^2 = (150 + πr^2)$ $cm^2$
								   =$150 + 22/7 ×4.2/2 × 4.2/2$ $cm^2$
								   =163.86 $cm^2$

Example: A wooden toy rocket is in the shape of a cone mounted on a cylinder, as shown in Fig. 13.8. The height of the entire rocket is 26 cm, while the height of the conical part is 6 cm. The base of the conical portion has a diameter of 5 cm, while the base diameter of the cylindrical portion is 3 cm. If the conical portion is to be painted orange and the cylindrical portion yellow, find the area of the rocket painted with each of these colours. (Take π = 3.14)


Solution : Denote radius of cone by $r$, slant height of cone by $l$, height of cone by $h$, radius of cylinder by $r′$ and height of cylinder by 4h′$.

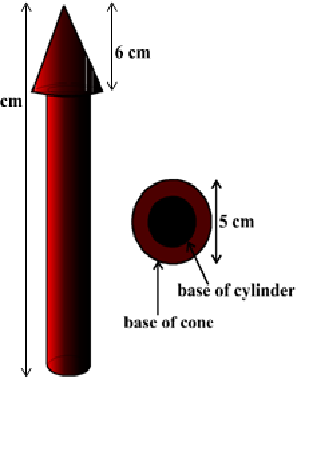
Then r = 2.5 cm, h = 6 cm, r′ = 1.5 cm, h′ = 26 – 6 = 20 cm and
$$l=√(r^2+h^2)$$

Here, the conical portion has its circular base resting on the base of the cylinder, but the base of the cone is larger than the base of the cylinder. So, a part of the base of the cone (a ring) is to be painted.

So, the area to be painted orange = CSA of the cone + base area of the cone – base area of the cylinder $${= πrl + πr^2 – π(r′)^2}$$ $${= π[(2.5 × 6.5) + (2.5)^2 – (1.5)^2] } cm^2$$ $$= π[20.25] cm^2 $$ $$= 63.585 cm^2$$

Now,the area to be painted yellow =  CSA of the cylinder + area of one base of the cylinder
				=  $2πr′h′  +  π(r′)^2$
				=  $πr′ (2h′ + r′)$
				=  (3.14 × 1.5) (2 × 20 + 1.5) $cm^2$
				=  4.71 × 41.5 $cm^2$
				=  195.465 $cm^2$ 
 
 

Example: Mayank made a bird-bath for his garden in  the  shape  of  a  cylinder  with  a  hemispherical
 depression at one  end (see Fig. 13.9). The height of the cylinder is 1.45 m and its radius is 30 cm. Find the 
 total surface area of the bird-bath. (Take π =  $22/7$  )  

 

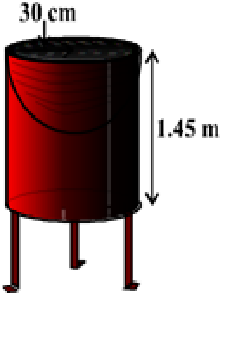
Solution : Let $h$ be height of the cylinder, and $r$ the common radius of the cylinder and hemisphere. 
			Then,the total surface area of the bird-bath =  CSA of cylinder + CSA of hemisphere
			=  $2πrh$ + $2πr^2$  = $2π r (h + r)$
			=   $22/7$ × 22 × 30(145 + 30) $cm^2$
			=  33000 $cm^2$   = 3.3 $m^2$