Behaviour of lines representing a pair of linear equations in two variables.
Consider a pair of lines represented by the equations :
Graphical Method of Solution of a Pair of Linear Equations
${a_1x + b_1y + c_1 = 0}$ and
${a_2x + b_2y + c_2 = 0}$
Hence, ${a_1x + b_1y + c_1 = 0}$ can be written as
$y=-{a_1/b_1}x-c_1/b_1$ .....................(1)
and ${a_2x + b_2y + c_2 = 0}$ can be written as
$y=-{a_2/b_2}x-c_2/b_2$ .....................(2)
We know that the standard equation of straight line is $y=mx+c$
where $m$ is the angle (slope) which the line make with $x-$ axis and $c$ is the intercept on $y-$ axis.
1)If the lines are parallel.
If the lines are parallel , then the slope of two lines are same but the intercept on $y-$ axis is different,i.e
$a_1/b_1=a_2/b_2$ and $c_1/b_1≠c_2/b_2$
i.e $a_1/a_2=b_1/b_2$ and $b_1/b_2≠c_1/c_2$
Hence,If the lines are parallel,the pair of linear equations has no solution, and is called an inconsistent pair of linear equations.
If the lines are parallel , then the slope of two lines are same but the intercept on $y-$ axis is different,i.e
$a_1/b_1=a_2/b_2$ and $c_1/b_1≠c_2/b_2$
i.e $a_1/a_2=b_1/b_2$ and $b_1/b_2≠c_1/c_2$
Hence,If the lines are parallel,the pair of linear equations has no solution, and is called an inconsistent pair of linear equations.
${a_1/a_2=b_1/b_2≠c_1/c_2}$e.g. ${x + 2y – 4 = 0}$ and ${2x + 4y – 12 =0 }$
2) If the lines are intersecting
If the lines are intersecting , then the slope of the lines are never equal , but the intercept on $y-$ axis can be equal.
i.e $a_1/b_1≠a_2/b_2$
i.e $a_1/a_2≠b_1/b_2$
Hence, if the lines are intersecting,then the pair of linear equations has one solution,and is called a consistent pair of linear equations.
If the lines are intersecting , then the slope of the lines are never equal , but the intercept on $y-$ axis can be equal.
i.e $a_1/b_1≠a_2/b_2$
i.e $a_1/a_2≠b_1/b_2$
Hence, if the lines are intersecting,then the pair of linear equations has one solution,and is called a consistent pair of linear equations.
${a_1/a_2≠b_1/b_2}$e.g. ${x – 2y = 0}$ and ${3x + 4y – 20 = 0}$
3) If the lines coincides (or are equivalent).
If the lines coincides, then the slope and intercept on $y-$ axis are same.
i.e $a_1/b_1=a_2/b_2$ and $c_1/b_1=c_2/b_2$
i.e $a_1/a_2=b_1/b_2$ and $b_1/b_2=c_1/c_2$
i.e $a_1/a_2=b_1/b_2=c_1/c_2$
Hence,the pair of linear equations has infinitely many distinct common solutions. Such a pair is called a dependent pair of linear equations in two variables. Note that a dependent pair of linear equations is always consistent.
If the lines coincides, then the slope and intercept on $y-$ axis are same.
i.e $a_1/b_1=a_2/b_2$ and $c_1/b_1=c_2/b_2$
i.e $a_1/a_2=b_1/b_2$ and $b_1/b_2=c_1/c_2$
i.e $a_1/a_2=b_1/b_2=c_1/c_2$
Hence,the pair of linear equations has infinitely many distinct common solutions. Such a pair is called a dependent pair of linear equations in two variables. Note that a dependent pair of linear equations is always consistent.
${a_1/a_2=b_1/b_2=c_1/c_2}$e.g. ${ 2x + 3y – 9 = 0}$ and ${4x + 6y – 18 = 0}$
${x + 3y = 6 }$ (1) and
${2x – 3y = 12}$ (2)
is consistent. If so, solve them graphically.
Solution : Let us draw the graphs of the Equations (1) and (2).
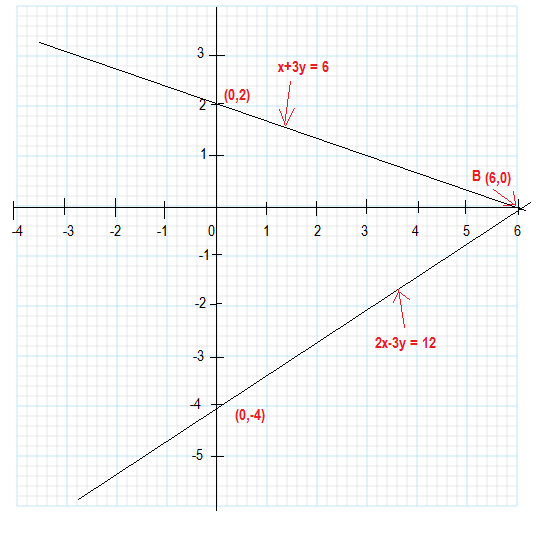
$x$ 0 6
y= (6-x)/3 2 0
$x$ 0 6
y=(12+2x)/3 -4 0
We observe that there is a point B (6, 0) common to both the lines AB and PQ.
So, the solution of the pair of linear equations is $x = 6$ and $y = 0$, i.e.,
the given pair of equations is consistent.
Example : Graphically, find whether the following pair of equations has no solution,
unique solution or infinitely many solutions:
${5x – 8y + 1 = 0 }$ (1)
${3x-24/5y+3/5=0}$ (2)
Solution : Multiplying Equation (2) by $5/3$ , we get
${3(5/3)x-24/5({5/3})y+3/5(5/3)=0}$
so we get,
${5x – 8y + 1 = 0}$
But, this is the same as Equation (1). Hence the lines represented by Equations (1)
and (2) are coincident. Therefore, Equations (1) and (2) have infinitely many solutions.
Solution : Let us denote the number of pants by $x$ and the number of skirts by $y$. Then the equations formed are :
The two lines intersect at the point (1, 0). So, $x = 1$, $y = 0$ is the required solution of the pair of linear
equations, i.e., the number of pants she purchased is 1 and she did not buy any skirt.
${y = 2x – 2}$ (1)
and ${y = 4x – 4}$ (2)
Draw the graphs of Equations (1) and (2) by finding two solutions for each of the equations.
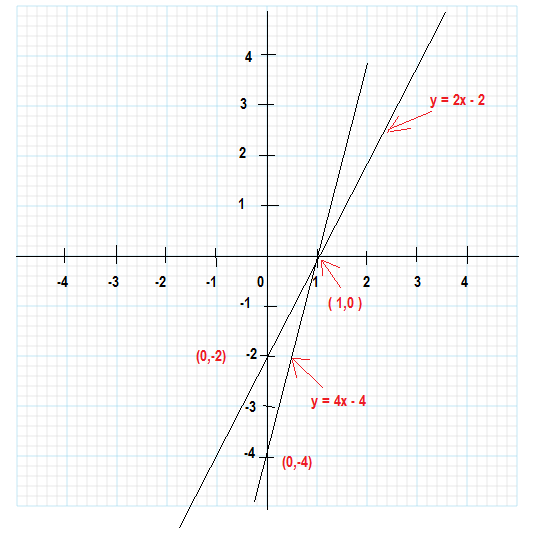
| $x$ | 0 | 1 |
| y= 2x – 2 | -2 | 0 |
| $x$ | 0 | 1 |
| y= 4x – 4 | -4 | 0 |
