Laravel

Chapters For Class X- CBSE


EXERCISE

1. Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.”
Represent this situation algebraically and graphically.

Solution
Let Aftab present age be = $x$ years
Let his daughter present age be = $y$ years
Condition 1: 7 years ago, Aftab age was  $x-7$ and his daughter age was $y-7$.
Since 7 years ago, Aftab age was 7 times of his daughter age then,
Hence  $x-7$ = 7($y-7$)  
       $x-7$ = ${7y-49}$
	   $x$   =${7y -42}$
	   $7y= x + 42$
	   $y= x/7 + 6$ 

Condition 2: 3 years from now, Aftab age will be $x+3$ and her daughter will be $y+3$
Given: 3 years from now Aftab shall be 3 times as old as his daughter will be. So,
		$x+3$ = 3($y+3$)
		$x/3+1$ = $y+3$
		$y=x/3 - 2$
	
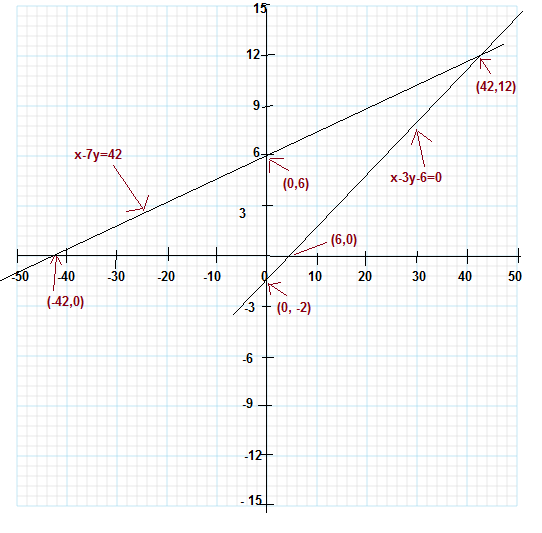
Algebraically representation:
		$x$   =${7y -42}$ ................(1)
		$x+3$ = 3($y+3$) ................(2)



Geometrically Representation:
   
         

		 
$x$0 -42 

		 
y= x/7 + 66 0 
		 
		 

		 
		 

		 
$x$0 6 

		 
y=x/3 - 2 - 2  0 
		 
		 

	Subsituting the value of $x$ from eqn (1) in eqn (2).

		${7y-42 + 3}$ =${3y+9}$
		
		    ${7y-39}$ =${3y+9}$
			${4y}$ =$48$
			$y=12$
			$x$ = ${7(12)-42}$ =42

Ans: Aftab present age = 42 years
       His daughter age = 12 years
2. The coach of a cricket team buys 3 bats and 6 balls for ₹ 3900. Later, she buys another bat and 3 more balls of the same kind for ₹ 1300. Represent this situation algebraically and geometrically. 

 Solution
 Let cost of one bat be ₹ $x$
 Cost of one ball be ₹ $y$
 
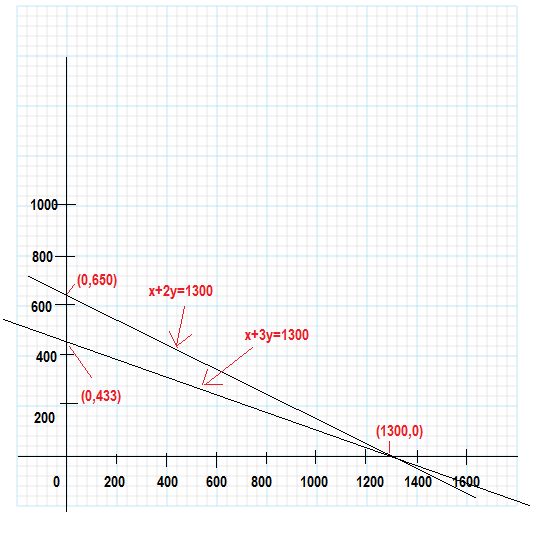
 Given: ${3x+6y=3900}$ i.e      $x+2y=1300$...................(1)
    and, ${x+3y=1300}$ ...................(2)
	
Solving eqn (1) and eqn (2)
 $x=1300$ 
 $y=0$

 Geometricaly representation:
  

		 
$x$ 0 1300 

		 
y= (1300-x)/2 650  0 
		 
		 

		 
		 

		 
$x$ 0   1300 

		 
y=(1300-x)/3 433.33  0
3. The cost of 2 kg of apples and 1kg of grapes on a day was found to be ₹ 160. After a month, the cost of 4 kg of apples and 2 kg of grapes is ₹ 300. Represent the situation algebraically and geometrically.

Solution
Let the cost of 1 kg apples = ₹ $x$
Let the cost of 1 kg grapes = ₹ $y$
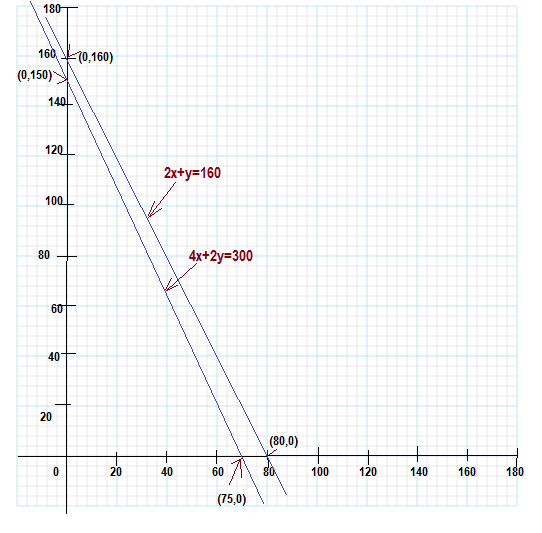
Therefore, $2x+1y= 160$ ..............(1) ,
and        $4x+2y=300 $ ...............(2)

Graphical representation .
  

		 
$x$0 80 

		 
y= 160 - 2x 160 0
		 
		 

		 
		 

		 
$x$0 75 

		 
y=(300 - 4x)/2 150  0